Octal and Hexadecimal Number

Complement of a Number   Types of Number system   Convert Decimal to Binary

If you are new to this article, I strongly recommend to read our previous article before preceding this. In our previous article, we had already seen that binary number has a base of 2. It means that binary number contains 2¹ = 2 combinations which are 0 and 1. Similarly, Octal and Hexadecimal number has a fixed number of combinations. As we earlier know that octal has a base 8, then it contains 8 digits through 0 to 7 which means 2³ =8 combinations and Hexadecimal has a base 16 which means it has 2⁴=16 combinations.

                If you are focusing on a sequence i.e. octal, hexadecimal. They are the combinations of increasing power of 2.

Octal – 2³ , Hexadecimal - 2⁴

This power indicates how many bits are in a number for a particular number system

Octal has 3 bits

Hexadecimal has 4 bits

This can be clear understand by following diagram-

 

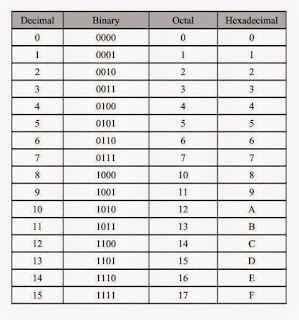
Explain – In this diagram, first we consider decimal number up to 7

You can clearly seen in this diagram that binary numbers has 0 at its first position, so you can write or remove this 0. Now if you remove this 0 than it has remaining only 3 binary bits which are [ 000, 001, 010, 011, 100, 101,110,111 ] these are the binary representation of octal Numbers [ 0, 1, 2, 3, 4, 5, 6, 7]

Now consider after 7 Number, binary number contains 1 at its first position, so we cannot remove this at its position, if we do not remove 1 at its position it contains 4 binary bits which are [ 0000, 0001, 0010, 0011, 0100, 0101, 0110, 0111, 1000, 1001, 1010, 1011, 1100, 1101, 1110, 1111] and these are the binary representation of Hexadecimal Number [ 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E, F]

Now we are ready to convert binary to octal, octal to binary, binary to hexadecimal, hexadecimal to binary. The following example illustrates the procedure :

( 10 110 001 101 011 . 111 100 000 110)2 = (26153.7406)8

   2    6     1     5     3   .   7     4    0      6

Conversion from binary to hexadecimal is similar, except that the binary number is divided into groups of four digits :

(10 1100 0110 1011 . 1111 0010)2 = (2C6B.F2)16

  2     C      6       B   .    F       2

Conversion from octal or hexadecimal to binary is done by a procedure reverse to the above.Each octal digit is converted to its 3-digit binary equivalent. Similarly, each hexadecimal digit is converted to its 4-digit binary equivalent. This is illustrated in the following examples:

(673.124)8 = (110 111 011 . 001 010 100)2

(306.D)16 = (0011 0000 0110 . 1101)2

« Previous   Complement of a Number »